Farah Baracat

Hwang, Kim & Park (2021) - Quantized Weight Transfer Method Using Spike-Timing-Dependent Plasticity for Hardware Spiking Neural Network

The paper can be found here.

Why am I reading about this topic?

I was curious to learn about how to convert a trained ANN to SNN. This approach is often mentioned in papers as an offline learning technique in which the synaptic weights are adjusted (well, surprise :D ) offline usually with gradient descent then transferred to the SNN. I started looking up how this is exactly accomplished with the goal of answering these questions:

• Is there a consensus on how to carry out the ANN to SNN conversion? is it a solved problem (the conversion I mean)?
• If so, what is the mathematical basis for this conversion?
• How to set the neuron’s threshold? more generally what happens to all these SNN parameters that do not have an ANN counterpart? are they trained? inferred? manually set?

Motivation

The goal of this paper is to create a hardware-based SNN used as an “inference system”. Here, the authors do not care about training or coming up with an online method but are solely focused on how to precisely map the offline-trained weights to what they call “synaptic devices” (i.e memristors).

Interlude on memristors (from the paper)

These devices change the synaptic weight between 2 neurons by adjusting the device conductance which occurs via its program (PGM) and erase (ERS) states. Therefore, to map a weight onto the hardware, PGM/ERS pulses are applied once or several times to reach the target synaptic conductance of the device.

Back to the main work

So what are the challenged to perform the above-mentioned conversion:

1. Low weight bit precision: while training offline, we usually use a full 32-bit precision floating point numbers. The synaptic devices have access to only limited discrete levels of conductance.
2. Scalability: according to the authors, the mapping process is time-consuming and hence do not scale well as the size of the network (i.e weights) increases. As described earlier, mapping a single weight corresponds to applying one or more pulses to an individual synaptic device, therefore, if I understood correctly, it would take time to repeat this process manually for each synaptic device one by one.

Main Contribution

Using STDP (Spike-Timing-Dependent PLasticity) to transfer quantized, trained ANN-weights to SNN synaptic weights implemented with memristor devices. The efficacy of the method is demonstrated on the MINST dataset.

The novelty of their approach, again according to the authors, lies in the use of STDP to adjust the synaptic conductance to match a target quantized weight. Usually, STDP is used to train the SNN. Here, it is exploited to map the weights to the hardware.

Methods

How can we operate their synaptic transistor?

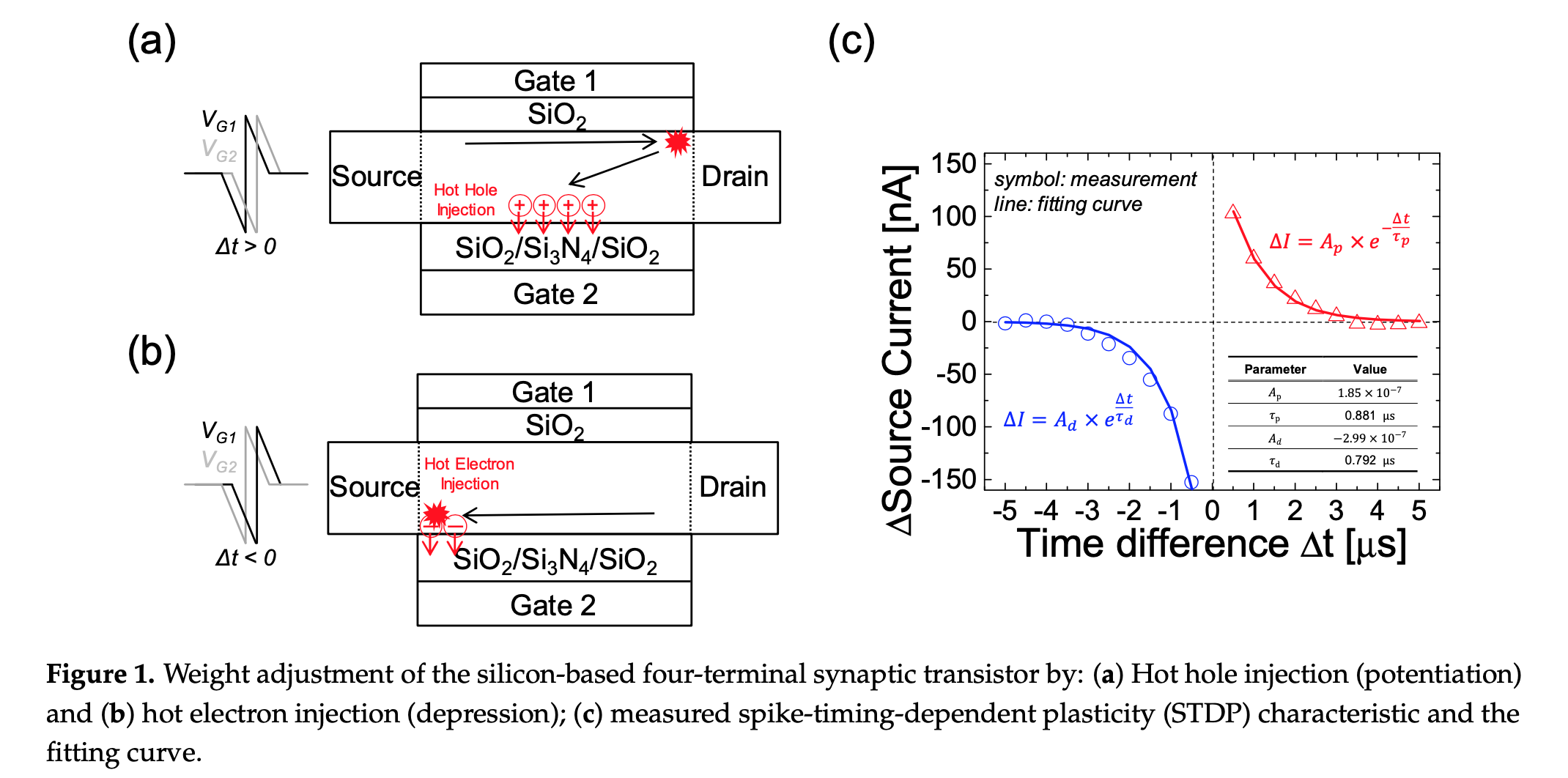
• The synaptic device used in this work is a 4-terminal transistor, fabricated in the same group. This paper describe the fabrication process. The device schematic is shown in Figure 1.

• The device has two gate terminals (Gate 1 and Gate 2). Depending on the time difference of the voltage pulse applied to Gate 1 and Gate 2 and the phenomenon of hot carrier injection, the device conductance is changed (demonstrated in the inset of Figure 1c in the changing source to drain current sign and amplitude).

• The authors note that the curve in inset Figure 1c resembles the STDP curves and therefore fit the curve with 2 STDP equations describing potentiation and depression. From these fit, they inferred the parameters of the STDP (i.e $A_p$, $A_d$, $\tau_p$ and $\tau_d$).

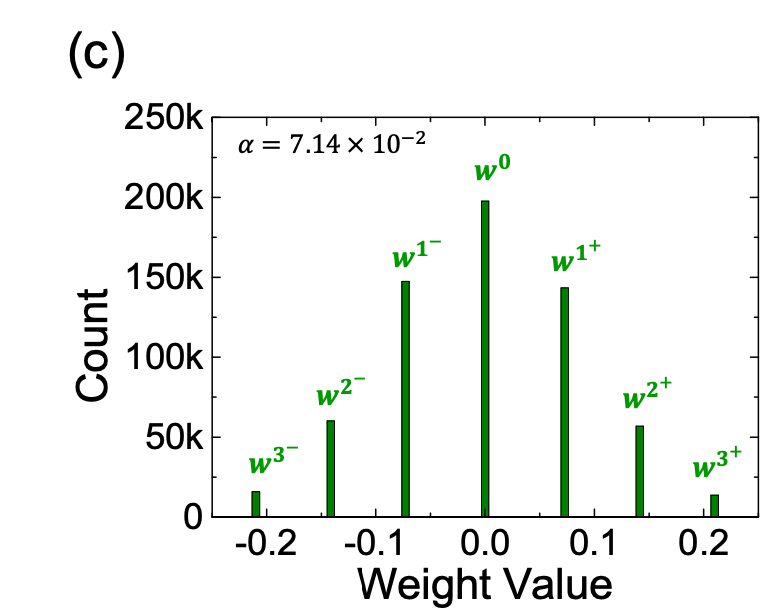
ANN trained on MNIST

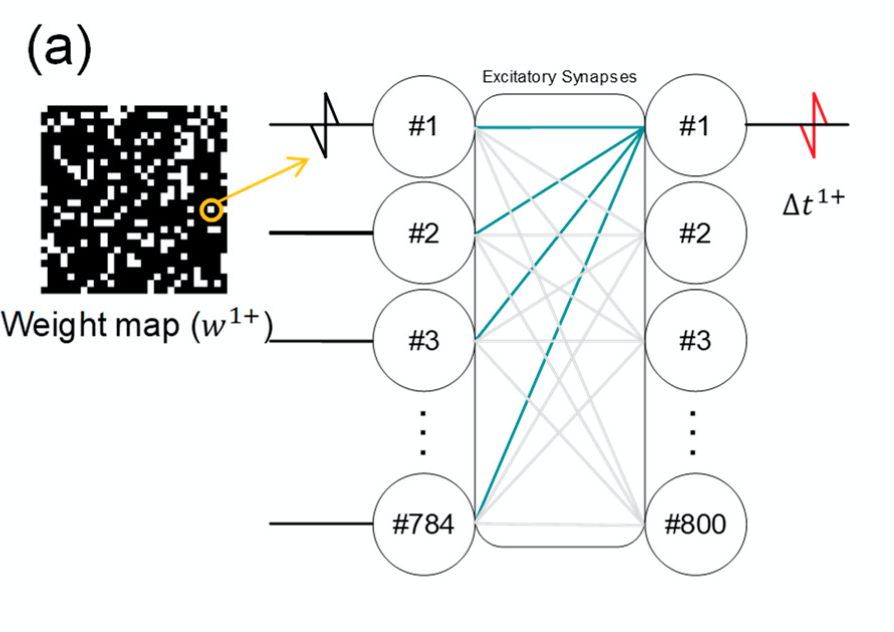
• 3-layer ANN with unit 784, 800 and 10 in the input, hidden and output layers is trained with stochastic gradient decent.
• Trained weights are normalized by the maximum output activation or maximum weight then quantized using a linear quantization method (weight distribution is equally divided into a linear scale): the weight distribution is divided by $2n+1$ level to cover both the negative and positive weights equally. See Figure below ($\alpha$ is the interval/distance between two levels).

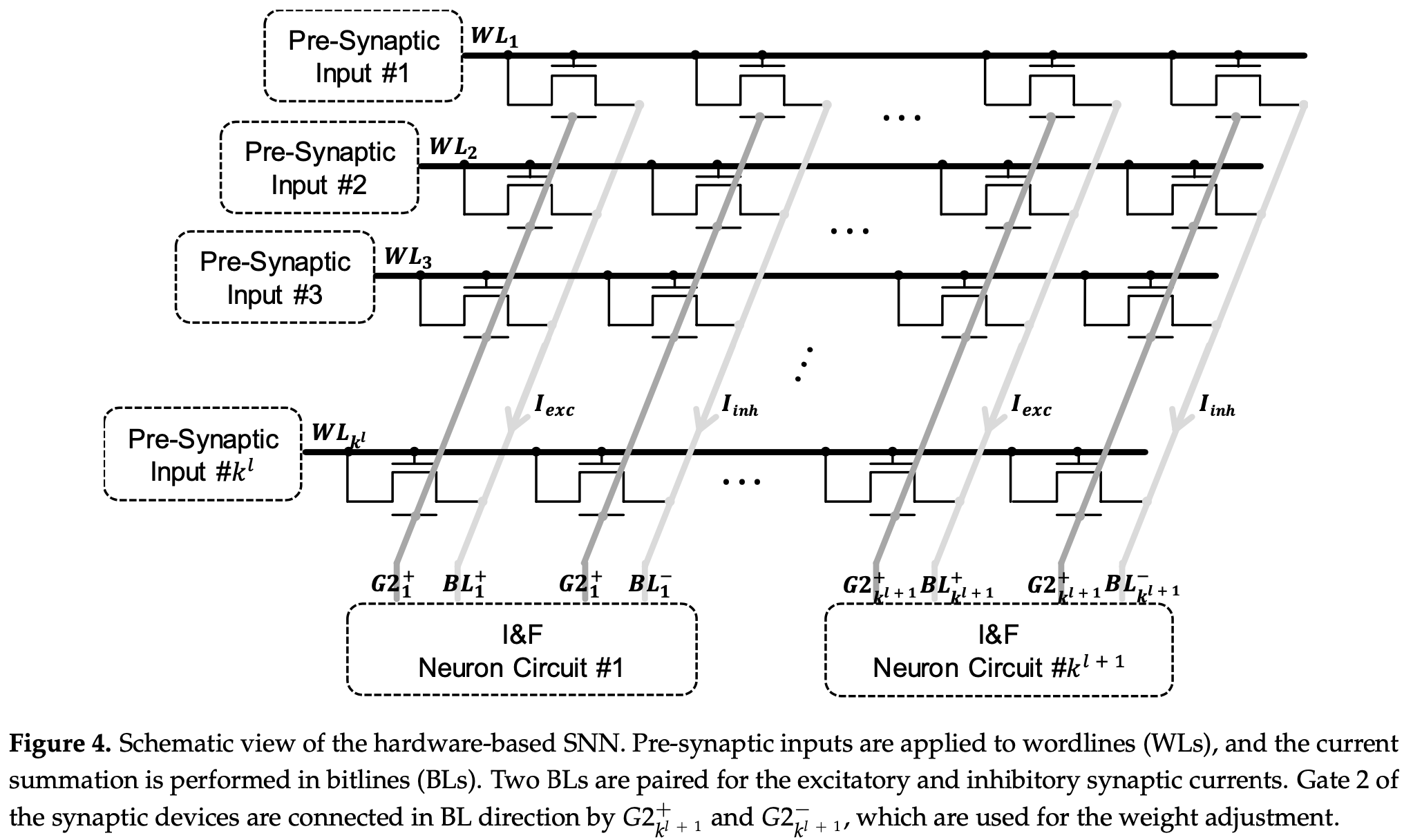
Hardware implementation of the SNN

• Synapses are arranged in an array (resembling a crossbar array 🤷🏼‍♀️).

• Each synaptic weight in the SNN is implemented by a pair of “synaptic transistors” (one excitatory and one inhibitory).

• Pre-synaptic inputs is applied to Gate 1 and drain terminals. Excitatory and inhibitory currents, $I_{exc}$ and $I_{inh}$ , flow through the bitlines (BL) (a strip connecting source terminals vertically) to the post-synaptic neuron $k^l$; where l is the $l^{th}$ layer. A neuron hence which receives two input currents, therefore $BL^+$ and $BL^-$.

• Gate 2 terminals are used for weight mapping only and are not used during inference.

Note that

• During inference, the label is predicted based on the neuron index with the maximum firing rate (as in most cases).
• Since the pre-synaptic input is connected to one of the Gate terminals, the weight is changed only when there is a pre-synaptic input.

Weight transfer by STDP

STDP is used to adjust the synaptic weighs “connected with the same BL simultaneously” in the following manner:

1. Find the exact pulse time difference, $\Delta t$, from the STDP equations obtained earlier.

2. Which synapse to change? since one synaptic weight is implemented by an excitatory and inhibitory synapse, the difference of the conductance of both synaptic devices represent this synaptic weight. They, therefore, only adjusted the excitatory synapse: $\Delta I_{source}= \Delta w$.

3. Apply the necessary voltage to the gates. Given a neuron in the hidden layer which is connected to 784 inputs (28x28), we can represent the synaptic weights to this neuron with a 4 different weight maps (assuming a 4-level quantization):

   • Each weight map consists of white and black dots, and corresponds to a quantized weight level.

   • Each white dot in the map represents the presence synaptic connection with this quantized weight between the input neuron (pixel) and the neuron in question.

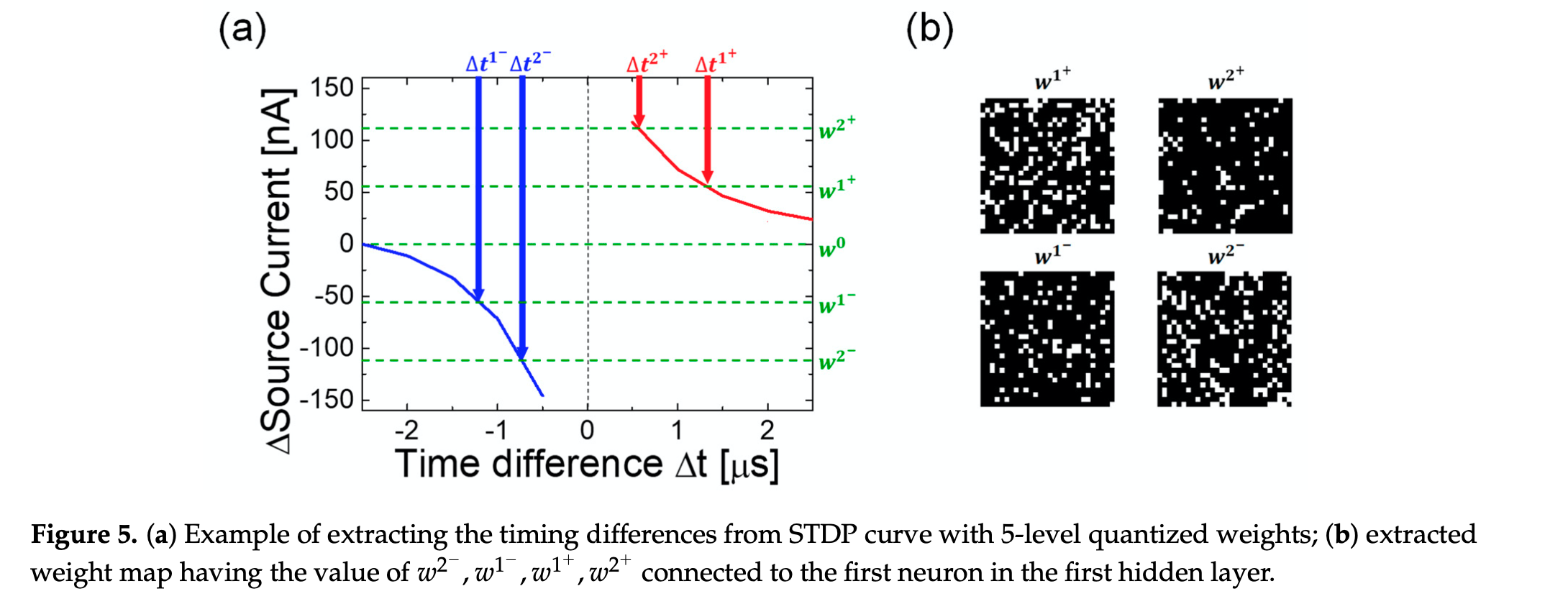
   Now if we activate the synapses connected to this neuron by applying a voltage-encoded input to Gate 1 of its pre-synaptic neurons (represented by white dots in the weight map) while providing an asymmetric voltage pulse (with the $\Delta t$ found in 1.) at Gate 2, we can then transfer one quantized weight (e.g. $w^{2+}$) to multiple synapses simultaneously.

4. If we then repeat the procedure in 3. for all the weight maps for each neuron in each layer, we can therefore modify all the synapses in the network.

Results

Performance accuracy is definitely impacted by the number of quantization levels used. Still, with 3-level quantization, accuracy was 97.58% (i.e close to the original 32-bit precision weights) with a noticeable reduction in the number of pulses required to map the weights onto the synaptic devices.

Final Thoughts

I am not familiar with this field of research, but it seems messy to me 😂 for 3 reasons:

1. The curve of the STDP is steep (which is desirable to achieve different conductance levels). Given that the pulse difference is in the order of few $\mu S$, I am wondering how precisely can we actually map the quantized weights.

2. I don’t quite understand why they used a pair of devices to encode a single weight and only programmed one 😏. Was it clear in the paper?

3. It is still not very obvious (to me at least) whether they considered device mismatch when fitting the STDP parameters. It was briefly mentioned that they also considered device mismatch in the simulations. However, results of these analyses are not shown. I assume that different devices would have different STDP parameters and hence $\Delta t$ values. It follows that we cannot transfer exactly the same weight to the different synapses simultaneously…right?

I can easily say though that this is not what I was looking for when searching for ANN to SNN conversion 😅: the work described in the paper is very specific to the hardware implementation while I was looking for a more general mathematical approach. Yet, I read the paper 😀 (because why not).